TRIGONOMETRY

LOS ANGULOS

Clasificación de ángulos según su medida

Agudo < 90°	Recto = 90°	Obtuso>90°
Convexo < 180°	Llano = 180°	Cóncavo > 180°
Nulo = 0º	Completo = 360°
Negativo < 0º	Mayor de 360°

Tipos de ángulos según su posición

Ángulos consecutivos

Ángulos consecutivos son aquellos que tienen el vértice y un lado común.

Ángulos adyacentes

Ángulos adyacentes son aquellos que tienen el vértice y un lado común, y los otros lados situados uno en polongación del otro.

Forman un ángulo llano.

Ángulos opuestos por el vértice

Son los que teniendo el vértice común, los lados de uno son prolongación de los lados del otro.

Los ángulos 1 y 3 son iguales.

Los ángulos 2 y 4 son iguales.

Clases de ángulos según su suma

Ángulos complementarios

Dos ángulos son complementarios si suman 90°.

Ángulos suplementarios

Dos ángulos son suplementarios si suman 180°.

Ángulos entre paralelas y una recta transversal

Ángulos correspondientes

 

Los ángulos 1 y 2 son iguales.

Ángulos alternos internos

 

Los ángulos 2 y 3 son iguales.

Ángulos alternos externos

 

Los ángulos 1 y 4 son iguales.

Ángulos en la circunferencia

Ángulo central

El ángulo central tiene su vértice en el centro de la circunferencia y sus lados son dos radios.

La medida de un arco es la de su ángulo central correspondiente.

Ángulo inscrito

El ángulo inscrito tiene su vértice está en la circunferencia y sus lados son secantes a ella.

Mide la mitad del arco que abarca.

Ángulo semiinscrito

El vértice de ángulo semiinscrito está en la circunferencia, un lado secante y el otro tangente a ella.

Mide la mitad del arco que abarca.

Ángulo interior

Su vértice es interior a la circunferencia y sus lados secantes a ella.

Mide la mitad de la suma de las medidas de los arcos que abarcan sus lados y las prolongaciones de sus lados.

Ángulo exterior

Su vértice es un punto exterior a la circunferencia y los lados de sus ángulos son: o secantes a ella, o uno tangente y otro secante, o tangentes a ella:

Mide la mitad de la diferencia entre las medidas de los arcos que abarcan sus lados sobre la circunferencia.

Ángulos de un polígono regular

Ángulo central de un polígono regular

Es el formado por dos radios consecutivos.

Si n es el número de lados de un polígono:

Ángulo central = 360° : n

Ángulo central del pentágono regular= 360° : 5 = 72º

Ángulo interior de un polígono regular

Es el formado por dos lados consecutivos.

Ángulo interior =180° − Ángulo central

Ángulo interior del pentágono regular = 180° − 72º = 108º

Ángulo exterior de un polígono regular

Es el formado por un lado y la prolongación de un lado consecutivo.

Los ángulos exteriores e interiores son suplementarios, es decir, que suman 180º.

Ángulo exterior = Ángulo central

Ángulo exterior del pentágono regular = 72º

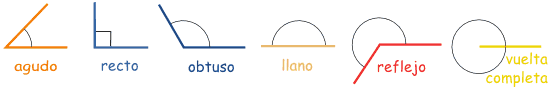
Cuidado con las medidas

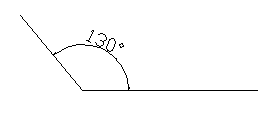
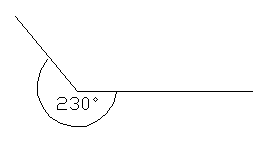
Este ángulo es obtuso.	Este ángulo es reflejo.
Pero las líneas son las mismas... así que cuando midas y marques ángulos, ¡asegúrate de que sabes cuál de los ángulos necesitas!

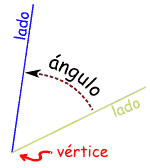Partes de un ángulo La esquina de un ángulo se llama vértice Y los lados rectos son rayos El ángulo es la cantidad de giro entre los dos rayos.

Marcar ángulos

Hay dos maneras comunes de marcar un ángulo:

1. dándole nombre, normalmente una letra minúscula como a o b, o a veces una letra griega como α (alfa) o θ (theta)

2. o con las tres letras que definen el ángulo, poniendo en medio la letra donde se encuentra (su vértice).

Ejemplo: el ángulo "a" es "BAC", y el ángulo "θ" es "BCD"

___________________________________________________________________________________

TEOREMA DEL COSENO 

De inmediato nos comentó de un nuevo teorema (Pesadilla II), diciendo: "En cualquier triángulo, el cuadrado de un lado es igual a la suma de los cuadrados de los otros dos lados menos el doble producto de estos dos lados por el coseno del ángulo que forman".

Quedamos claritos (¿?). Osea utilizando la siguiente figura con sus elementos queda algo así:

a² = b² + c² - 2bc cos a

b² = a² + c² - 2ac cos b

c² = a² + b² - 2ac cos g

Y la orden que no se hizo esperar: Demuestren que lo que les dije es verdad. (Plop!)

A mover nuevamente nuestras neuronas.

Comenzamos trazando la altura h_c del triángulo ABC dado y designamos por p y q los segmentos formados por esta altura.

Si observamos bien, en el triángulo DBC obtenemos, por Pitágoras, obviamente, que:

h_c² + p² = a²  o sea:

h_c² = a² - p²

mientras que el triángulo ADC determinamos que:

h_c² + q² = b²  o sea:

h_c² = b² - q²

Estos pasos nos llevan a la conclusión que a² - p² = b² - q² lo que implica que

a² = b² - q² + p²

pero p = c - q, lo que al reemplazar en la expresión anterior permite obtener que:

a² = b² - q² + (c - q)² , desarrollando resulta a² = b² - q² + c² - 2cq + q² , simplificando:

 a² = b² + c² - 2cq , pero cos a = q/b de donde q = b cos a.

Luego  a² = b² + c² - 2bc cos a

Las otras demostraciones te las dejamos de tarea, como venganza (je, je , je risa macabra) por todo lo que tuvimos que sufrir para demostrar lo anterior.

Vamos a un ejemplo:

Determinemos la longitud de c en el triángulo ABC de la figura:

c² = a² + b² - 2ab cos g

c² =

c² = 8

c =

___________________________________________________________________________________

TEOREMA DEL SENO

Teorema del seno

De Wikipedia, la enciclopedia libre

 

Saltar a: navegación, búsqueda

Teorema del seno.

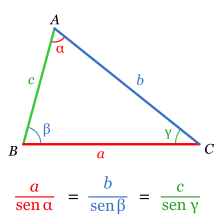
En trigonometría, el teorema del seno es una relación de proporcionalidad entre las longitudes de los lados de un triángulo y los senos de los ángulos respectivamente opuestos.

Usualmente se presenta de la siguiente forma:

Teorema del seno Si en un triángulo ABC, las medidas de los lados opuestos a los ángulos A, B y C son respectivamente a, b, c, entonces:

https://www.youtube.com/watch?v=GiS_LzYxhWo

______________________________________________________________________________

FUNCIONES TRIGONOMÉTRICAS

En matemáticas, las funciones trigonométricas son las funciones establecidas con el fin de extender la definición de las razones trigonométricas a todos los números reales y complejos.

Las funciones trigonométricas son de gran importancia en física, astronomía, cartografía, náutica, telecomunicaciones, la representación de fenómenos periódicos, y otras muchas aplicaciones.

https://www.youtube.com/watch?v=FKYk5BBXf_A

___________________________________________________________________________________

FUNCION CUADRATICA

https://www.youtube.com/watch?v=IAQ2CVjcW2I

 

 

En matemáticas, una función cuadrática o función de segundo grado es una función polinómica definida como:

Gráficas de funciones cuadráticas.

1. redirección Función cuadrática

Una función cuadrática es aquella que puede escribirse de la forma: f(x) = ax2 + bx + c donde a, b y c son números reales cualesquiera y a distinto de cero.

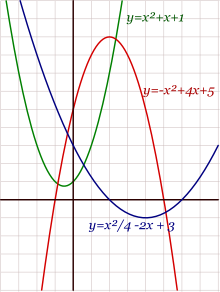
Si representamos "todos" los puntos (x,f(x)) de una función cuadrática, obtenemos siempre una curva llamada parábola.

Como ejemplo, ahí tienes la representación gráfica de dos funciones cuadráticas muy sencillas: f(x) = x2 f(x) = -x2

Primer forma para sacar la raíz: 1) se iguala la ecuación a cero. 2) se factoriza la ecuación. 3)cada factor se iguala a cero.

Para graficar la función: 1)se determina si la parábola abre hacia arriba o hacia abajo. 2)obtener los puntos de intesección en el eje x, es decir obtener las raíces de la ecuación. 3)obtener el vértice de la función ya sea por medio de punto medio o utilizando la formula -b/2a. 4)graficar los puntos obtenidos en los puntos 1 y 2 graficar la curva.

Caso especial: si la función es x2 siempre pasa por el origen f(x)=x2-4 f(x)=(x+2)(x-2) x+2=0 x-2=0 x=-2 x=2

Punto medio (-2+2)/2=0

Sustituye valores f(0)=(o*o)-4=-4

Archivo:Sin título

 

en donde a, b y c son números reales (constantes) y a es distinto de 0.

La representación gráfica en el plano cartesiano de una función cuadrática es una parábola, cuyo eje de simetría es paralelo al eje de las ordenadas. La parábola se abrirá hacia arriba si el signo de a es positivo, y hacia abajo en caso contrario. El estudio de las funciones cuadráticas tiene numerosas aplicaciones en campos muy diversos, como por ejemplo la caída libre o el tiro parabólico.

La derivada de una función cuadrática es una función lineal y su integral una función cúbica.

___________________________________________________________________________________

 LINKOGRAFIA:

https://es.wikipedia.org/wiki/Funci%C3%B3n_cuadr%C3%A1tica

https://thales.cica.es/rd/Recursos/rd99/ed99-0416-02/indice.htm

______________________________________________________________________________

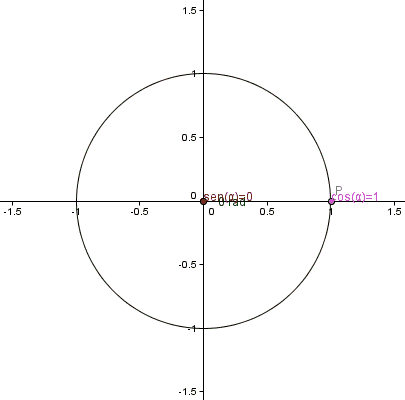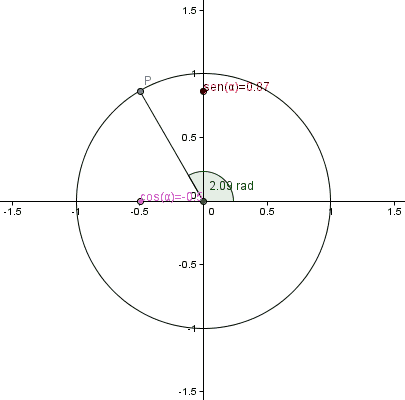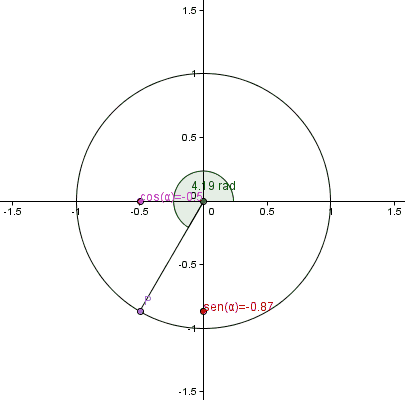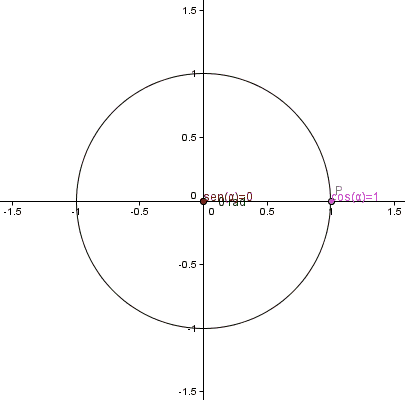
GRAFICA DE FUNCIONES TRIGONOMETRICAS

Graficar las funciones seno, coseno y tangente.

1.dibujar la circunferencia

2.ubicar los angulos cada 15°

3.pasar las medidas de los angulos de grados a radianes.

4. ubicar las medidas de los angulos en radianes en la circunferencia unitaria.

5. trazar la escala.

______________________________________________________________________________

ANGULO POSITIVO Y ANGULO NEGATIVO

ANGULO POSITIVO:

un angulo es positivo cuando al ubicarlo en posicion normal su medida se toma en el sentido contrario de las manecillas del reloj.

ANGULO NEGATIVO:

Un angulo es negativo cuando al ubicarlo en posicion normal su medida se toma igual a las manecillas del reloj.

Ángulo negativo

El ángulo negativo mide menos de 0º.

Los ángulos negativos giran en el sentido horario, es decir, en el sentido en que se mueven las agujas de un reloj.

Un ángulo negativo lo podemos transformar en un ángulo positivo sumándole 360º.

-α = 360° - α

Razones trigonométricas del ángulo negativo

______________________________________________________________________________

 Conversion de grados a radianes